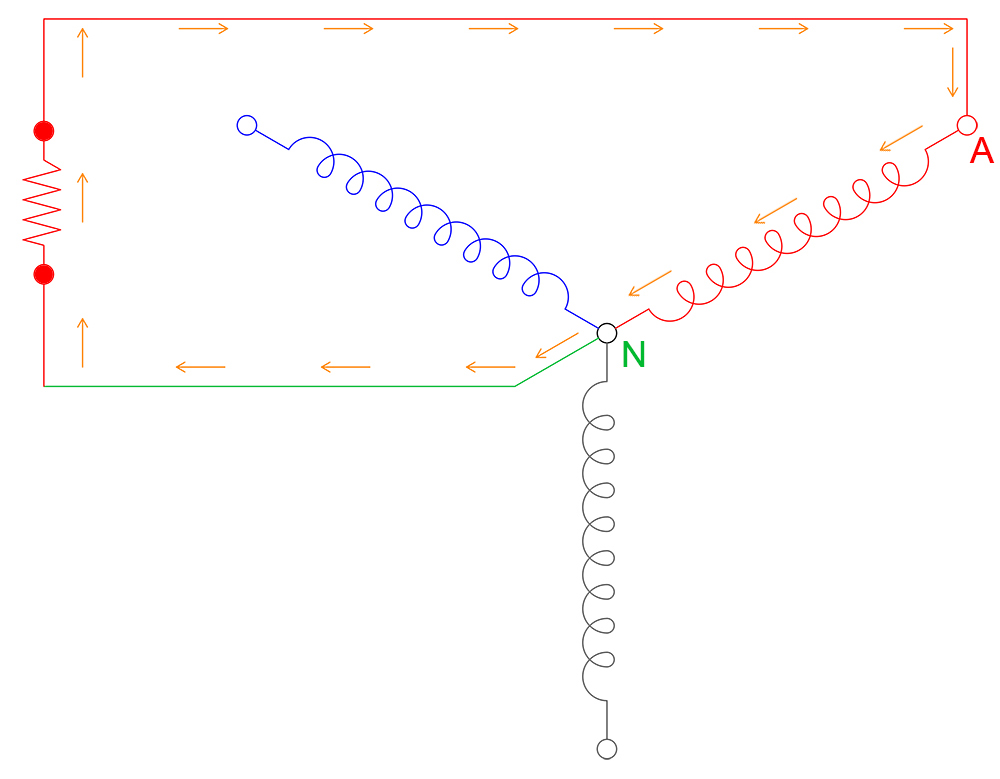
Why does the Line Voltage lead the Phase Voltage in a 3-Phase Wye?

If you follow the orange arrows on the diagram below starting at Point A it moves through the phase windings to Point N and then from Point N through the load to back to Point A.

This means that the Line A voltage is the phasor sum of V_AN and V_NA.

V_A = V_AN + V_NA.

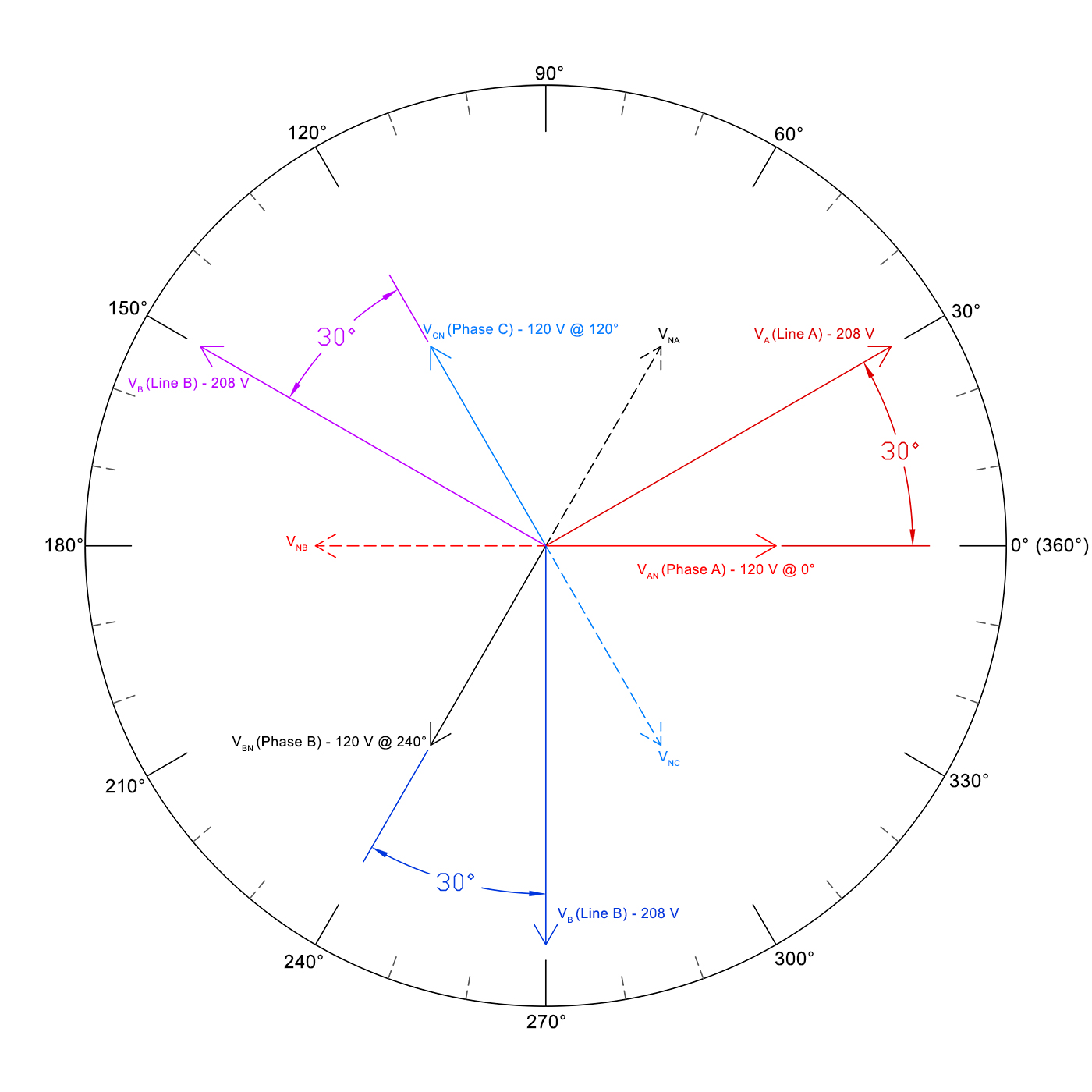
The Line Voltage V_AB (Line A) is the phasor sum of of V_AN and V_NA. V_NA is the same magnitude as V_BN but with the opposite polarity.

Phase A = 120 V @ 0° | Phase NA = 120 V @ 180°

Phase B = 120 V @ 240° | Phase NA = 120 V @ 60°

Phase C = 120 V @ 120° | Phase NC = 120 V @ 300°

Knowing this, let's find the Line Current for Line A.

V_A = V_AN + N_NA

V_A = 120 V @ 0° + 120 V @ 60°

	Horizontal	Vertical
VAN = 120 @ 0°	120.0000000	0.0000000
VNA = 120 @ 60°	60.0000000	103.9230485
Totals	180.0000000	103.9230485

Using Pythagorean Theorem, we know that C² = A² + B²

Line A² = 180² + 103.9230485²

Line A² = 43,200.00001

Line A = 207.8460969

Now we just need to determine the angle that Line A is at. To do this, we take our Total Horizontal Value (180) and divide that by our Line A value (207.8460969).

Pf_A = Horizontal Total / Line A

Pf_A = 180 / 207.8460969

Pf_A = 0.865900421

Line A ∠ = cos^-1(0.865900421)

Line A ∠ = 30.01431877

V_A = 207.8460969 @ 30.01431877° OR (208 V @ 30°)

Below is a phasor diagram that shows the three phases, their corresponding inverse phases and the Line Voltages.